تدریس ریاضی

مساحت ذوزنقه محاطی و محیطی
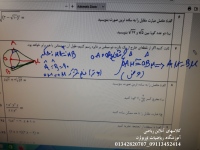
یک ذوزنقه هم دارای یک دایره محاطی باشد (تمام ضلع‌ها مماس بر دایره) و هم در یک دایره محاطی شده باشد (تمام رئوس روی دایره باشند) یا دقیقتر سوال هندسه 2 اینطوریه که اگر یک ذوزنقه ای داشته باشیم که هم محیطی و هم محاطی باشه, مساحت آن از میانگین حسابی دو قاعده ضرب در میانگین هندسی بدست می آید.
محاطی بود یعنی خودش در دل یک دایره قرار دارد و محیطی بودن یعنی یک دایره در دل خودش قرار دارد.
می دانیم که مساحت یک ذوزنقه از رابطه قاعده بالا بعلاوه قاعده پایین ضرب در ارتغاعش بدست می آید تقسیم بر 2.

ذوزنقه متساوی‌الساقین است: ذوزنقه‌ای که در یک دایره محاط شود، باید متساوی‌الساقین باشد (ساق‌های آن هم‌اندازه باشند).
شرط وجود دایره محاطی: یک چهارضلعی (از جمله ذوزنقه) دارای دایره محاطی است اگر و فقط اگر مجموع طول‌های اضلاع مقابل آن با هم برابر باشند. در مورد ذوزنقه ABCD با قاعده‌های AB و CD و ساق‌های AD و BC، این شرط به صورت AB+CD=AD+BC خواهد بود.
بنابراین، یک ذوزنقه که هم محیطی باشد و هم محاطی، یک ذوزنقه متساوی‌الساقین است که در آن مجموع طول‌های قاعده‌ها با مجموع طول‌های ساق‌ها برابر است.
لطفا به مطالب دقیقتر این فیلم آموزشی گوش نمائید تا آسانتر به حل سوالات تقریبا سخت اینچنینی در هندسه 2 مسلط شوید.
اگه شما هم سوالات شبیه این در پایه های مختلف ریاضیات و هندسه دارید و می خواهید به جواب صحیح برسید, با ما تماس گرفته و با پرداخت مبلغی به آموزشگاه ریاضیات توربو لرن, دریافت نمائید و اگر به معلم خصوصی آنلاین اینترنتی هم نیازمند بودید, با شماره تلفن های زیر تماس بگیرید.
01342820707_09113452414
ادامه تدریس این سوال را در یوتیوب ما ببینید: https://youtu.be/EsrHYtjix_8