تدریس ریاضی

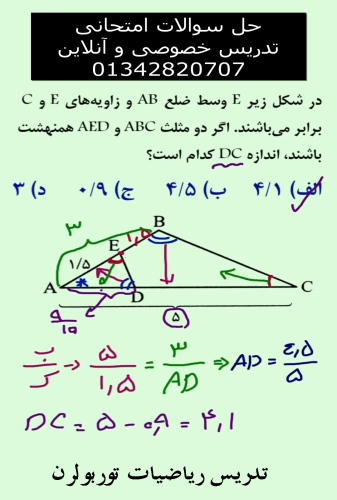
هم‌نهشتی مثلث‌ها (Congruence of Triangles) یعنی دو مثلث دقیقاً اندازه و شکل یکسان داشته باشند، یعنی همه ضلع‌ها و همه زاویه‌های متناظرشان برابر باشند و بتوان یکی را با حرکت صلب (چرخش، جابجایی یا قرینه کردن) روی دیگری گذاشت تا کاملاً منطبق شوند.

در پایه هفتم، چهار شرط اصلی (معیار) برای اثبات هم‌نهشتی دو مثلث آموزش داده می‌شود که فقط با دانستن سه مقدار خاص می‌توان گفت دو مثلث هم‌نهشت هستند. این چهار معیار عبارتند از:

1. SAS (ضلع–زاویه–ضلع) اگر دو ضلع و زاویه بین آن‌ها (زاویه محصور) در یک مثلث با دو ضلع و زاویه بین آن‌ها در مثلث دیگر برابر باشد، دو مثلث هم‌نهشت هستند. ترتیب مهم است: ضلع → زاویه بین → ضلع دوم.
2. SSS (ضلع–ضلع–ضلع) اگر هر سه ضلع یک مثلث با هر سه ضلع مثلث دیگر برابر باشد، دو مثلث هم‌نهشت هستند. (این قوی‌ترین معیار است چون فقط به طول ضلع‌ها نگاه می‌کند.)
3. ASA (زاویه–ضلع–زاویه) اگر دو زاویه و ضلع بین آن‌ها (ضلع محصور) در یک مثلث با دو زاویه و ضلع بین آن‌ها در مثلث دیگر برابر باشد، دو مثلث هم‌نهشت هستند.
4. AAS (زاویه–زاویه–ضلع) اگر دو زاویه و ضلعی که بین آن‌ها نیست (یعنی یکی از ضلع‌های غیرمحصور) در یک مثلث با دو زاویه و همان ضلع غیرمحصور در مثلث دیگر برابر باشد، دو مثلث هم‌نهشت هستند. (توجه: چون مجموع زاویه‌های مثلث 180 درجه است، اگر دو زاویه برابر باشند، زاویه سوم هم خودبه‌خود برابر می‌شود.)

معیارهایی که در پایه هفتم پذیرفته نیستند (اشتباه رایج دانش‌آموزان):

• AAA: فقط سه زاویه برابر باشد کافی نیست! (چون مثلث‌ها می‌توانند شبیه باشند ولی اندازه‌شان متفاوت باشد → تشابه، نه هم‌نهشتی)
• SSA: دو ضلع و زاویه غیرمحصور برابر باشد، همیشه هم‌نهشتی نمی‌دهد (ممکن است دو حالت یا هیچ حالت نداشته باشد → به آن «حالت مبهم» می‌گویند).

نکته مهم برای اثبات در پایه هفتم:

وقتی می‌خواهید هم‌نهشتی دو مثلث را بنویسید، از علامت ≅ استفاده می‌کنید و حتماً رئوس را به ترتیب متناظر می‌نویسید. مثال: △ABC ≅ △DEF یعنی A متناظر D، B متناظر E، C متناظر F است پس ضلع AB = DE، زاویه B = زاویه E و غیره.

خلاصه چهار معیار معتبر پایه هفتم:

• SAS → ضلع–زاویه بین–ضلع
• SSS → سه ضلع
• ASA → زاویه–ضلع بین–زاویه
• AAS → زاویه–زاویه–ضلع غیربین

با دانستن یکی از این چهار حالت، می‌توانید بگویید دو مثلث کاملاً برابر و هم‌نهشت هستند.

برای دیدن فیلم آموزشی سوالات مربوط به همنهشتی مثلث ها روی همین مطللب ضربه بزنید.