تدریس ریاضی

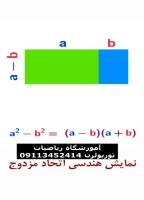
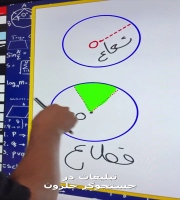
اثبات قضیه استوارت در هندسه پایه یازدهم
قضیه استوارت بیان می کند که در هر مثلث ABC، اگر D نقطه ای روی ضلع BC باشد، آنگاه رابطه زیر برقرار است:

b2m+c2n=a(d2+mn)

که در آن:

a طول ضلع BC است.
b طول ضلع AC است.
c طول ضلع AB است.
d طول پاره خط AD است.
m طول پاره خط BD است.
n طول پاره خط DC است.

اثبات این قضیه (Stewart's theorem) معمولاً با استفاده از قانون کسینوس ها در مثلث های ABD و ACD انجام می شود. با در نظر گرفتن زاویه های مجاور ضلع AD و استفاده از رابطه بین #کسینوس یک زاویه و کسینوس مکمل آن، می توان معادلات را دستکاری کرد تا به رابطه مورد نظر رسید. روش دیگر برای اثبات این قضیه استفاده از قضیه #فیثاغورس با رسم ارتفاع از راس A به ضلع BC است. با نوشتن طول اضلاع b، c و d بر حسب ارتفاع و قطعات ایجاد شده روی ضلع BC، می توان با دستکاری جبری به قضیه استوارت رسید.
برای حل سوالات هندسه و ریاضیات و داشتن معلم خصوصی آنلاین از سراسر جهان می توانید با ما تماس بگیرید.
01342820707_09113452414
آموزشگاه ریاضیات توربولرن: https://youtu.be/8SegPxzm5rg