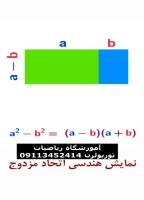
تدریس ریاضی

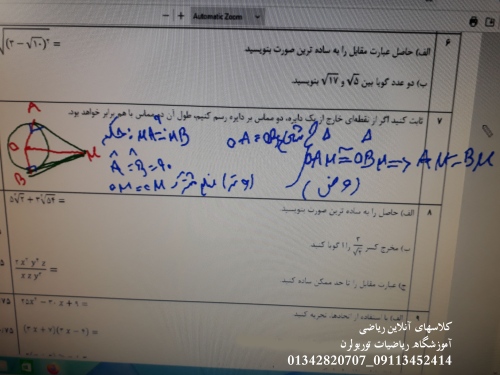
حل سوالات امتحانی ریاضی پایه نهم مربوط به دایره ها

سوال: ثابت کنید اگر از نقطه ای خارج از یک دایره, دو مماس بر دایره رسم کنیم, طول آن دو مماس با هم برابر خواهد بود.

برای اثبات این که اگر از نقطه‌ای خارج از یک دایره، دو مماس به دایره رسم کنیم، طول این دو مماس برابر است، می‌توانیم از خواص هندسی دایره و مماس‌ها استفاده کنیم. در ادامه، اثبات را به صورت گام به گام و با زبانی ساده ارائه می‌دهم:

صورت مسئله:

فرض کنید دایره‌ای با مرکز O و شعاع  r داریم. نقطه‌ای به نام  P در خارج از دایره قرار دارد. از نقطه P ، دو مماس به دایره رسم شده است که نقاط تماس آن‌ها با دایره  A و  B هستند. باید ثابت کنیم که طول مماس‌ها، یعنی PA=PB PA = PB PA=PB، برابر است.

اثبات:

1. تعریف مماس و خواص آن:
   • مماس از نقطه  P به نقطه  A خطی است که دایره را در نقطه  A لمس می‌کند و عمود بر شعاع  OA است. بنابراین، ∠OAP=90∘ angle OAP = 90^circ ∠OAP=90∘.
   • به طور مشابه، مماس از نقطه P P P به نقطه B B B عمود بر شعاع OB OB OB است، یعنی ∠OBP=90∘ angle OBP = 90^circ ∠OBP=90∘.
2. بررسی مثلث‌های △OAP triangle OAP △OAP و △OBP triangle OBP △OBP:
   • در مثلث △OAP triangle OAP △OAP:
     •  OA شعاع دایره است، بنابراین OA=r OA = r OA=r.
     • ∠OAP=90∘ angle OAP = 90^circ ∠OAP=90∘ (چون PA PA PA مماس است).
     •  OP ضلع مشترک بین دو مثلث است.
   • در مثلث △OBP triangle OBP △OBP:
     • OB=r OB = r OB=r (چون OB OB OB نیز شعاع دایره است).
     • ∠OBP=90∘ angle OBP = 90^circ ∠OBP=90∘ (چون PB PB PB مماس است).
     •  OP همان ضلع مشترک است.
3. مقایسه مثلث‌ها:
   • هر دو مثلث △OAP triangle OAP △OAP و △OBP triangle OBP △OBP قائم‌الزاویه هستند (زاویه 90∘ 90^circ 90∘ در A A A و B B B).
   • اضلاع OA=OB=r OA = OB = r OA=OB=r (شعاع‌های دایره).
   • ضلع  OP در هر دو مثلث مشترک است.
4. نتیجه‌گیری از تشابه مثلث‌ها:
   • با توجه به اینکه هر دو مثلث قائم‌الزاویه هستند و دو ضلع برابر دارند (OA=OB OA = OB OA=OB و  OP مشترک)، بر اساس قضیه فیثاغورس یا معیار تشابه (مثلث‌های قائم‌الزاویه با اضلاع برابر)، می‌توان گفت که △OAP≅△OBP triangle OAP cong triangle OBP △OAP≅△OBP (مثلث‌ها متشابه و در واقع هم‌نهشت هستند).
5. برابری اضلاع متناظر:
   • چون مثلث‌ها هم‌نهشت هستند، اضلاع متناظر آن‌ها برابرند. ضلع PA PA PA در △OAP triangle OAP △OAP متناظر با ضلع PB PB PB در △OBP triangle OBP △OBP است. بنابراین: PA=PBPA = PBPA=PB

نتیجه:

طول دو مماس  PA و  PB که از نقطه  P خارج از دایره به نقاط تماس  A و B روی دایره رسم شده‌اند، برابر است.

توضیح تکمیلی:

این نتیجه از خواص هندسی مماس‌ها و دایره ناشی می‌شود و نیازی به محاسبات پیچیده ندارد. همچنین، این ویژگی در مسائل هندسی و کاربردهای عملی مانند طراحی و مهندسی بسیار مفید است.

برای مشاهده مطالب مربوط به دایره روی همین خط کلیک نمائید.

برای دیدن فیلم آموزشی حل همین سوال, روی این خط ضربه بزنید

کلاسهای آنلاین ریاضی
آموزشگاه ریاضیات توربولرن
01342820707_09113452414