تدریس ریاضی

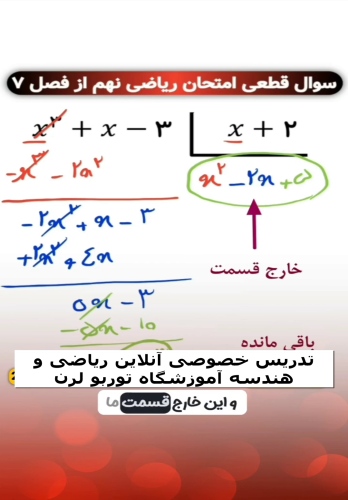
در فصل هفتم کتاب ریاضی نهم، یکی از پرتکرارترین و مهم‌ترین نوع سوالات امتحانات نهایی و آزمون‌های مدارس، سوالاتی است که از شما می‌خواهد یک چندجمله‌ای را بر چندجمله‌ای دیگر بخش کنید و خارج قسمت و باقی‌مانده را پیدا کنید.

این سوالات معمولاً به چهار شکل می‌آیند:

1. سوال مستقیم تقسیم (مثل کتاب تمرین صفحه 104 و 105) مثال کلاسیک: «چندجمله‌ای 3x⁴ − 5x³ + 4x − 2 را بر (x² − 2x + 1) تقسیم کنید.» جواب: خارج قسمت می‌شود 3x² + x + 2 و باقی‌مانده صفر است.

2. سوالاتی که باقی‌مانده را داده و یکی از چندجمله‌ای‌ها را نمی‌دهد پرطرفدارترین شکل در امتحان نهایی سال‌های اخیر: «هرگاه چندجمله‌ای P(x) را بر (x−2) تقسیم کنیم باقی‌مانده 5 و بر (x+3) تقسیم کنیم باقی‌مانده −7 به دست می‌آید. اگر P(x) بر (x−2)(x+3) بخش‌پذیر باشد، P(x) را بیابید.» روش حل سریع: فرض می‌کنیم P(x) = (x−2)(x+3)(ax + b) بعد دو معادله می‌سازیم و a و b را پیدا می‌کنیم.

3. سوالاتی که می‌گوید «باقی‌مانده عددی است» مثال: «P(x) را بر (x² + x − 6) تقسیم کردیم، خارج قسمت Q(x) و باقی‌مانده 4x − 3 شد. P(x) را بیابید.» روش: طبق قضیه تقسیم می‌نویسیم P(x) = (x² + x − 6) Q(x) + 4x − 3 حالا چون درجه باقی‌مانده باید کمتر از درجه مقسوم‌علیه باشد (اینجا درجه 1)، درست است. برای پیدا کردن Q(x) معمولاً چند مقدار برای x می‌گذاریم یا ضرایب را مقایسه می‌کنیم.

4. سوال ترکیبی با دستگاه معادلات مثلاً: «هرگاه P(x) را بر x² − 1 تقسیم کنیم باقی‌مانده −3x + 5 به دست می‌آید و هرگاه بر x² + 4x + 3 تقسیم کنیم باقی‌مانده 2x − 1 می‌شود. P(x) کدام است؟» روش طلایی: P(x) = (x² − 1) Q₁(x) − 3x + 5 P(x) = (x² + 4x + 3) Q₂(x) + 2x − 1 بعد دو طرف را برابر می‌گذاریم و چون x² − 1 و x² + 4x + 3 تقریباً هم‌درجه‌اند، معمولاً Q₁(x) و Q₂(x) را ثابت فرض می‌کنیم یا از روش جایگذاری x=1 و x=−1 و x=−3 استفاده می‌کنیم.

چند نکته طلایی که 90٪ سوالات این مدلی را حل می‌کند:

• اگر مقسوم‌علیه درجه 2 باشد، باقی‌مانده حتماً درجه کمتر از 2 یعنی خطی یا ثابت است (ax + b یا فقط عدد).
• اگر گفته «بخش‌پذیر است» یعنی باقی‌مانده صفر و حتماً مقسوم‌علیه عامل مقسوم است.
• در امتحان نهایی معمولاً یکی از ریشه‌های مقسوم‌علیه را در P(x) جایگذاری می‌کنند تا باقی‌مانده به دست بیاید (قضیه باقی‌مانده).
• برای پیدا کردن چندجمله‌ای ناشناخته، همیشه به صورت P(x) = (مقسوم‌علیه) × چیزی) + باقی‌مانده بنویسید.

با تمرین فقط 10 تا از این مدل سوال، دیگر هیچ سوال چندجمله‌ای به چندجمله‌ای در امتحان نهایی نمی‌تواند شما را غافلگیر کند. کافی است شکل سوال را تشخیص دهید و یکی از چهار روش بالا را سریع اجرا کنید!

لطفا برای دیدن تدریس سوالات نهایی چندجمله‌ای پایه نهم, روی همین نوشته ضربه بزنید.