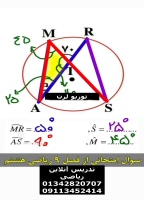
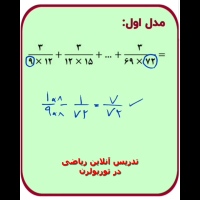
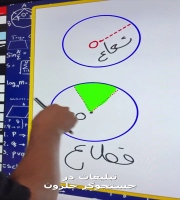
تدریس ریاضی

آموزش ساده و ریاضی: چگونه مجموعه اعداد اول را بنویسیم؟

اعداد اول، آن اعداد جادویی و خاص ریاضی هستند که فقط بر 1 و خودشان بخش‌پذیرند. یعنی هیچ عدد دیگری نمی‌تواند آن‌ها را بدون باقی‌مانده تقسیم کند. مثلاً 2، 3، 5، 7، 11، 13، 17 و غیره.

حالا چطور مجموعه تمام اعداد اول را به صورت ریاضی و دقیق بنویسیم؟

1. ساده‌ترین و رایج‌ترین روش: توصیف با کلمات
این روش در کتاب‌های درسی و مقالات خیلی استفاده می‌شود:

«مجموعه اعداد اول، مجموعه تمام اعداد طبیعی بزرگ‌تر از 1 است که تنها دو مقسوم‌علیه مثبت دارند: خودشان و 1.»

یا به صورت نمادین:

[ P = { n in mathbb{N} mid n > 1 text{ و } n text{ اول باشد} } ]

2. روش دقیق‌تر با استفاده از تقسیم‌پذیری (تعریف ریاضی رسمی)
[ P = { n in mathbb{N} mid n > 1 text{ و } forall d in mathbb{N} : (1 < d < n Rightarrow d nmid n) } ]

یعنی: مجموعه‌ای از اعداد طبیعی بزرگ‌تر از 1 که هیچ مقسوم‌علیه طبیعی بین 2 تا n-1 ندارند.

3. روش خلاصه و زیبا برای نمایش مجموعه
[ P = { 2, 3, 5, 7, 11, 13, 17, 19, 23, dots } ]

این نقطه‌چین نشان می‌دهد که مجموعه ادامه دارد و بی‌نهایت است (همان قضیه معروف اقلیدس که می‌گوید تعداد اعداد اول نامتناهی است).

4. روش پیشرفته‌تر (برای دانشجویان یا علاقه‌مندان به نظریه اعداد)
می‌توانیم از تابع نشانگر اول بودن استفاده کنیم:

[ P = { n in mathbb{N} mid n > 1 text{ و } pi(n) - pi(n-1) = 1 } ]

که π(n) تعداد اعداد اول تا n است، ولی این روش کمی پیچیده است و بیشتر برای محاسبات کامپیوتری استفاده می‌شود.

نکته‌های مهم و جالب:
- 2 تنها عدد اول زوج است.
- هر عدد اول بزرگ‌تر از 2، حتماً فرد است.
- هیچ فرمول ساده‌ای برای تولید همه اعداد اول وجود ندارد (اگر بود، جایزه بزرگی می‌برد!).

پس اگر بخواهید در یک مقاله، کتاب یا چت ریاضی بنویسید، کافی است بگویید:

«اعداد اول = مجموعه ( P = { 2, 3, 5, 7, 11, 13, dots } )، اعداد طبیعی بزرگ‌تر از 1 که هیچ مقسوم‌علیه طبیعی به جز 1 و خودشان ندارند.»

همین! ساده، دقیق و کاملاً ریاضی.

برای دیدن فیلم آموزشی نوشتن مجموعه تمام اعداد اول را به صورت ریاضی و دقیق بنویسیم؟ روی همین خط کلیک نمائید.