تدریس ریاضی

قدر مطلق |x| چیست؟ کامل، ساده و یونیک برای پایه نهم

قدر مطلق (Absolute value) یک عدد، یعنی فاصلهٔ آن عدد از صفر روی محور اعداد، و فاصله همیشه مثبت یا صفر است.

به زبان خیلی ساده: |x| = همیشه ≥ 0 یعنی هیچ‌وقت منفی نمی‌شود!

تعریف رسمی به دو شکل:

1. اگر x ≥ 0 باشد → |x| = x
2. اگر x < 0 باشد → |x| = −x (یعنی علامت منفی را برمی‌داریم)

مثال: |7| = 7 |−5| = 5 |0| = 0

خواص خیلی مهم قدر مطلق (این‌ها را حفظ کن، همیشه سر امتحان می‌آیند!)

1. |−a| = |a| → قدر مطلق عدد منفی و مثبت یکسان است
2. |a| × |b| = |a × b| → علامت ضرب داخل قدر مطلق می‌آید بیرون
3. |a| ÷ |b| = |a ÷ b| (به شرط b ≠ 0)
4. |a + b| ≤ |a| + |b| → نابرابری مثلث (خیلی مهم!)
5. |a − b| ≥ ||a| − |b|| → نابرابری مثلث برعکس
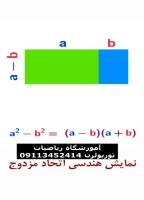
6. |a|² = a² → قدر مطلق را مربع کنی یا عدد را اول مربع کنی فرقی ندارد
7. √(a²) = |a| → جذر همیشه مثبت است، پس برابر قدر مطلق می‌شود

حل معادله قدر مطلقی (پایه نهم)

الف) |x| = 5 یعنی فاصلهٔ x از صفر برابر 5 است → دو جواب: x = 5 یا x = −5

ب) |x − 3| = 4 یعنی فاصلهٔ x از عدد 3 برابر 4 است → دو حالت: x − 3 = 4 → x = 7 x − 3 = −4 → x = −1

ج) |x + 2| = 0 فقط یک جواب: x + 2 = 0 → x = −2

د) |x − 1| = −3 هیچ جوابی ندارد! چون قدر مطلق هیچ‌وقت منفی نمی‌شود.

حل نامعادله قدر مطلقی

1. |x| < 4 یعنی فاصلهٔ x از صفر کمتر از 4 → −4 < x < 4
2. |x| ≤ 7 −7 ≤ x ≤ 7
3. |x − 2| ≤ 5 یعنی فاصلهٔ x از 2 حداکثر 5 واحد → −5 ≤ x − 2 ≤ 5 −3 ≤ x ≤ 7
4. |x + 1| > 3 x + 1 > 3 یا x + 1 < −3 x > 2 یا x < −4

ترفند طلایی برای معادلات پیچیده‌تر (نهم خیلی می‌آید)

م)

مثال: |2x − 6| = 8 اول داخل قدر مطلق را ساده کن: |2(x − 3)| = 8 چون |2| × |x − 3| = 8 2|x − 3| = 8 |x − 3| = 4 حالا دو حالت: x − 3 = 4 → x = 7 x − 3 = −4 → x = −1

چند مثال ترکیبی باحال و چالشی

1. |x + 3| + |x − 2| = 5 اینجا باید نقاط بحرانی را پیدا کنیم (جایی که داخل قدر مطلق صفر می‌شود): x = −3 و x = 2 محور را به سه قسمت تقسیم می‌کنیم:

• اگر x < −3: (−x − 3) + (−x + 2) = 5 → −2x − 1 = 5 → x = −3 (که در بازه نیست)
• اگر −3 ≤ x < 2: (x + 3) + (−x + 2) = 5 → 5 = 5 (همی همهٔ این بازه جواب است)
• اگر x ≥ 2: (x + 3) + (x − 2) = 5 → 2x + 1 = 5 → x = 2

جواب نهایی: [−3, 2]

1. |x² − 4| = 3 x² − 4 = 3 یا x² − 4 = −3 x² = 7 x² = 1 x = ±√7 x = ±1

جملهٔ قشنگ پایانی که هیچ‌وقت فراموش نکنی:

«قدر مطلق (Absolute value) مثل یه آینه است: هر چی بهش بدی، فقط جنبهٔ مثبتش رو نشون میده، حتی اگه خود عدد غمگین و منفی باشه!»

حالا برو همهٔ تست‌های قدر مطلق نهم رو بزن زمین!

برای دیدن فیلم تدریس قدر مطلق روی همین خط ضربهربزنید.