تدریس ریاضی

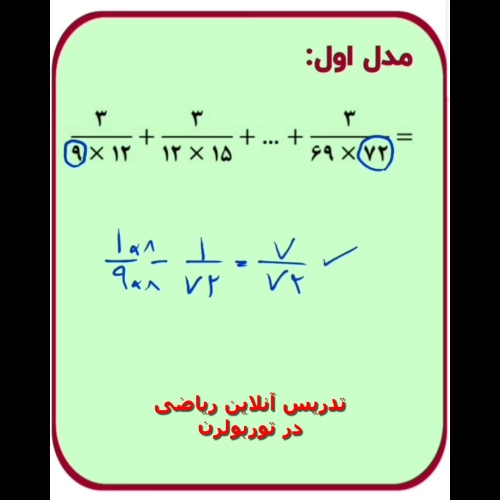
آموزش حل کسرهای تلسکوپی در ریاضیات: راهنمایی گام‌به‌گام

کسرهای تلسکوپی (Telescoping Fractions) یکی از تکنیک‌های هوشمندانه در ریاضیات هستند که اغلب در محاسبه مجموع سری‌ها، انتگرال‌گیری جزئی (Partial Fractions) و اثبات نابرابری‌ها به کار می‌روند. ویژگی اصلی آن‌ها این است که پس از تجزیه، بیشتر جملات در مجموع یکدیگر را حذف می‌کنند و فقط چند جمله ابتدایی و انتهایی باقی می‌ماند – درست مثل یک تلسکوپ که جمع و باز می‌شود!

کسر تلسکوپی چیست؟
یک کسر تلسکوپی معمولاً به شکلی است که می‌توان آن را به صورت تفاوت دو عبارت نوشت:
[
frac{1}{n(n+k)} = frac{1}{k} left( frac{1}{n} - frac{1}{n+k} right)
]
یا به طور کلی‌تر:
[
f(n) - f(n+1) quad text{یا} quad f(n-1) - f(n)
]
وقتی مجموع چنین کسرهایی را از n=1 تا n=N (یا تا بی‌نهایت) حساب کنیم، بیشتر جملات میانی حذف می‌شوند.

مثال کلاسیک 1: مجموع هارمونیک جزئی
یکی از معروف‌ترین مثال‌ها، تفاوت مجموع هارمونیک است:
[
sum_{n=1}^{N} left( frac{1}{n} - frac{1}{n+1} right)
]
بیایید آن را بنویسیم:
[
left( frac{1}{1} - frac{1}{2} right) + left( frac{1}{2} - frac{1}{3} right) + left( frac{1}{3} - frac{1}{4} right) + cdots + left( frac{1}{N} - frac{1}{N+1} right)
]
می‌بینید که جملات -frac{1}{2} و +frac{1}{2}، -frac{1}{3} و +frac{1}{3} و ... حذف می‌شوند. فقط جمله اول مثبت و جمله آخر منفی باقی می‌ماند:
[
sum_{n=1}^{N} left( frac{1}{n} - frac{1}{n+1} right) = 1 - frac{1}{N+1} = frac{N}{N+1}
]
وقتی N به بی‌نهایت برود، مجموع برابر 1 می‌شود.

مثال 2: مجموع sum frac{1}{n(n+1)}
ابتدا کسر را تجزیه می‌کنیم:
[
frac{1}{n(n+1)} = frac{1}{n} - frac{1}{n+1}
]
(این همان مثال بالاست!) پس:
[
sum_{n=1}^{N} frac{1}{n(n+1)} = sum_{n=1}^{N} left( frac{1}{n} - frac{1}{n+1} right) = 1 - frac{1}{N+1} = frac{N}{N+1}
]

مثال 3: مجموع گسترده‌تر sum frac{1}{n(n+k)}
فرض کنید k عدد طبیعی ثابت باشد. تجزیه:
[
frac{1}{n(n+k)} = frac{1}{k} left( frac{1}{n} - frac{1}{n+k} right)
]
پس مجموع:
[
sum_{n=1}^{N} frac{1}{n(n+k)} = frac{1}{k} sum_{n=1}^{N} left( frac{1}{n} - frac{1}{n+k} right)
]
= frac{1}{k} left[ left( frac{1}{1} + frac{1}{2} + cdots + frac{1}{k} right) - left( frac{1}{N+1} + frac{1}{N+2} + cdots + frac{1}{N+k} right) right]
]
وقتی N به بی‌نهایت برود، جملات دوم به صفر میل می‌کنند و مجموع برابر frac{H_k}{k} می‌شود که H_k مجموع هارمونیک تا k است.

مثال 4: سری با تفاوت مربعات
[
frac{1}{n(n+1)(n+2)} = frac{1}{2} left( frac{1}{n(n+1)} - frac{1}{(n+1)(n+2)} right)
]
این را می‌توان با انتگرال‌گیری جزئی به دست آورد. سپس مجموع دوباره تلسکوپی می‌شود.

چطور خودمان تجزیه کنیم؟
روش استاندارد برای تجزیه کسرهای گویا به شکل تلسکوپی استفاده از **انتگرال‌گیری جزئی (Partial Fraction Decomposition) است:
1. کسر را به صورت مجموع کسرهای ساده بنویسید.
2. ضرایب را پیدا کنید.
3. ببینید آیا می‌توان آن را به شکل تفاوت دو تابع نوشت.

اگر مخرج چندجمله‌ای خطی و درجه یک بیشتر از صورت باشد، معمولاً تلسکوپی می‌شود.

کاربردها
- محاسبه دقیق مجموع سری‌های خاص بدون نیاز به حدهای پیچیده.
- اثبات نابرابری‌ها (مثل نابرابری هارمونیک).
- حل مسائل المپیاد ریاضی.
- در حساب دیفرانسیل و انتگرال برای محاسبه انتگرال‌های خاص.
هر وقت در مجموع سری با کسرهای گویا برخورد کردید، ابتدا سعی کنید آن را به شکل تفاوت بنویسید. اگر بیشتر جملات حذف شدند، یعنی تلسکوپی است! تمرین مداوم روی مثال‌های مختلف بهترین راه یادگیری این تکنیک قدرتمند است.

با تمرین این روش، حل بسیاری از مسائل سری و دنباله برایتان بسیار ساده و زیبا خواهد شد. موفق باشید!

برای دیدن فیلم حل کسرهای تلسکوپی روی همین نوشته کلیک کنید.