تدریس ریاضی

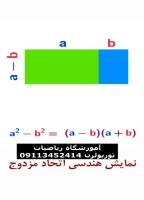
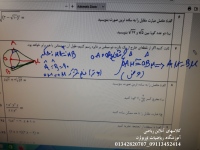
وضعیت دو دایره مماس درونی در هندسه یازدم و دوازدهم
ضمن توجه به مطالب این مبحث آموزشی, و دقت در مطالب گفته شده ما در طول فیلم, نوشته های کلی وضعیت دو دایره در هندسه (The situation of two circles in geometry) را بخوانید.
در هندسه، دو دایره مماس درونی وضعیتی را توصیف می‌کنند که در آن یک دایره در داخل دایره دیگر قرار دارد و هر دو دقیقاً در یک نقطه با هم تماس دارند. در این حالت، دایره کوچکتر در داخل دایره بزرگتر قرار می‌گیرد و تنها یک نقطه مشترک بین آن‌ها وجود دارد که به آن نقطه تماس می‌گویند.

ویژگی‌های دو دایره مماس درونی:

یک نقطه تماس مشترک: دو دایره دقیقاً در یک نقطه با هم مشترک هستند.
قرارگیری: مرکز دایره کوچکتر و مرکز دایره بزرگتر در یک طرف خط مماس مشترک در نقطه تماس قرار دارند.
فاصله بین مراکز: فاصله بین مراکز دو دایره مماس درونی برابر با قدر مطلق تفاضل شعاع‌های آن‌ها است. اگر R شعاع دایره بزرگتر و r شعاع دایره کوچکتر باشد، و d فاصله بین مراکز آن‌ها باشد، آنگاه: d=∣R−r∣ از آنجایی که دایره کوچکتر درون دایره بزرگتر است، معمولاً R بزرگترr در نظر گرفته می‌شود، بنابراین: d=R−r
مماس مشترک: دو دایره مماس درونی فقط یک مماس مشترک دارند که در نقطه تماس بر هر دو دایره مماس است. این خط در نقطه تماس بر خطی که از مراکز دو دایره می‌گذرد عمود است.

تصور هندسی:
تصور کنید یک سکه کوچکتر را داخل یک بشقاب بزرگتر قرار داده‌اید به طوری که لبه‌های آن‌ها در یک نقطه با هم تماس پیدا کرده‌اند. این وضعیت نشان‌دهنده دو دایره مماس درونی است.

کاربردها:
مفهوم دو دایره مماس درونی در مسائل مختلف هندسی و طراحی کاربرد دارد. به عنوان مثال، در طراحی لوگوها، الگوها و همچنین در حل مسائل مربوط به دایره‌ها و مماس‌ها در هندسه تحلیلی و اقلیدسی.
لطفا با سابسکرایپ و لایک و نظرات تان و ارسال این مطالب به سایر دوستانتان در رشد ریاضیات و هندسه مارا یاری نمائید. #ریاضی_دوازدهم #ریاضی_یازدهم
تلفن تماس با آموزشگاه ریاضیات توربولرن: 01342820707_09113452414
دیدن این فیلم آموزش در یوتیوب ما: https://youtube.com/shorts/HCjoZ_OuaGU