تدریس ریاضی

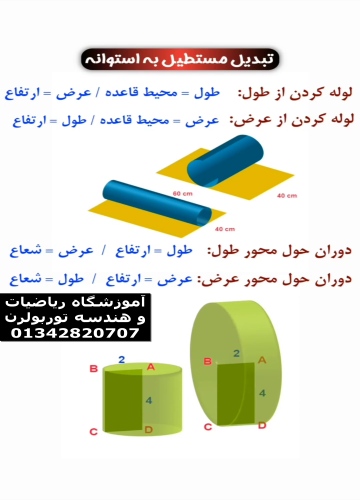
تبدیل مستطیل به استوانه: یک سفر هندسی خلاقانه

تصور کنید یک برگ کاغذ مستطیلی معمولی در دست دارید. این مستطیل فقط یک شکل مسطح نیست؛ پتانسیل تبدیل شدن به یک جسم سه‌بعدی شگفت‌انگیز را دارد: استوانه! این تبدیل یکی از زیباترین ایده‌های هندسه است که نشان می‌دهد چگونه یک سطح دوبعدی می‌تواند بدون کشیده شدن یا پاره شدن، به یک حجم سه‌بعدی تبدیل شود.

گام‌های تبدیل (به شیوه‌ای که خودتان بتوانید امتحان کنید):

1. انتخاب وجه مستطیل برای تبدیل شدن به ارتفاع استوانه مستطیل دو ضلع بلندتر (طول) و دو ضلع کوتاه‌تر (عرض) دارد. تصمیم بگیرید کدام ضلع «ارتفاع» استوانه آینده خواهد شد. معمولاً ضلع کوتاه‌تر را به عنوان ارتفاع انتخاب می‌کنیم تا استوانه بلندتر و زیباتر شود.

2. چرخاندن و چسباندن یکی از ضلع‌های انتخاب‌شده برای ارتفاع را ثابت نگه دارید و ضلع مقابل آن را به سمتش بچرخانید تا دقیقاً روی هم قرار بگیرند. حالا دو ضلع ارتفاع کاملاً روی هم افتاده‌اند و مستطیل به یک لوله بدون درپوش تبدیل شده است. این لوله همان سطح جانبی استوانه است.

3. تشکیل قاعده‌ها دو ضلع باقی‌مانده مستطیل (که قبلاً طول بودند) حالا به صورت دو دایره کاملاً برابر در دو انتهای لوله درآمده‌اند. این دو دایره، قاعده‌های بالایی و پایینی استوانه هستند.

نکته جالب: در این تبدیل، هیچ نقطه‌ای از کاغذ از جای خود جدا نمی‌شود و هیچ چین اضافی ایجاد نمی‌شود؛ فقط خم می‌شود. به همین دلیل می‌گوییم سطح جانبی استوانه «همسان» (isometric) با مستطیل اولیه است، یعنی مساحتشان دقیقاً برابر است.

چرا این تبدیل مهم است؟

• مساحت سطح جانبی: مساحت مستطیل اولیه دقیقاً برابر است با مساحت سطح جانبی استوانه نهایی. اگر طول مستطیل lll و عرض آن www باشد و www را به عنوان ارتفاع استوانه انتخاب کنیم، آنگاه محیط قاعده استوانه برابر lll و شعاع آن r=l2πr = frac{l}{2pi}r=2πl​ خواهد بود. مساحت جانبی هم 2πr×w=l×w2pi r times w = l times w2πr×w=l×w است؛ دقیقاً مساحت مستطیل!
• حفظ طول و زاویه: در این تبدیل، تمام فاصله‌ها و زاویه‌های قائمه روی سطح حفظ می‌شوند. اگر روی مستطیل یک شبکه شطرنجی بکشید و سپس آن را به استوانه تبدیل کنید، مربع‌های شبکه روی سطح استوانه به شکل لوزی‌های منظم درمی‌آیند، اما طول اضلاع و زاویه‌های بین خطوط متقاطع همچنان همان است.

یک آزمایش ذهنی جذاب

فرض کنید روی مستطیل یک خط مورب از گوشه پایین چپ به گوشه بالا راست بکشید. پس از تبدیل به استوانه، این خط مورب به یک مارپیچ منظم (هلیس) روی سطح استوانه تبدیل می‌شود. اگر ارتفاع استوانه دقیقاً برابر محیط قاعده باشد (یعنی مستطیل مربع باشد)، این مارپیچ دقیقاً یک دور کامل می‌زند و به زیباترین شکل ممکن خود می‌رسد.

این تبدیل ساده نه تنها پایه محاسبات سطح و حجم استوانه است، بلکه دریچه‌ای به دنیای هندسه غیراقلیدسی و توپولوژی هم باز می‌کند؛ جایی که می‌فهمیم «مسطح بودن» و «خمیده بودن» گاهی فقط به نحوه نگاه ما بستگی دارد.

دفعه بعد که یک برگ کاغذ مستطیلی دیدید، لحظه‌ای مکث کنید و به پتانسیل پنهان آن برای تبدیل شدن به یک استوانه کامل فکر کنید. هندسه همیشه در ساده‌ترین اشیاء اطرافمان مخفی شده است!

برای دیدن فیلم آموزشی تبدیل مستطیل به استوانه در هندسه, روی همین نوشته ضربه بزنید.