تدریس ریاضی

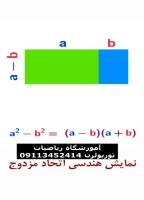
جمع بندی سوالات هندسه یک ترم اول یا امتحانات نهایی مثل مکان هندسی
جمع‌بندی سوالات هندسه ترم اول و امتحانات نهایی، به‌ویژه در مبحث مکان هندسی، نیازمند دسته‌بندی و بررسی دقیق مفاهیم کلیدی است. در اینجا به برخی از مهم‌ترین نکات و سوالات پرتکرار در این زمینه اشاره می‌کنیم:

مفاهیم کلیدی مکان هندسی:
تعریف مکان هندسی: مجموعه‌ای از نقاط که در یک یا چند شرط هندسی مشترک هستند.
انواع مکان‌های هندسی:
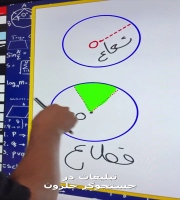
دایره: مکان هندسی نقاطی که از یک نقطه ثابت (مرکز) به فاصله ثابت (شعاع) هستند.
خط عمود منصف: مکان هندسی نقاطی که از دو نقطه ثابت به یک فاصله هستند.
نیم‌ساز زاویه: مکان هندسی نقاطی که از دو ضلع زاویه به یک فاصله هستند.
سهمی: مکان هندسی نقاطی که از یک خط ثابت (خط هادی) و یک نقطه ثابت (کانون) به یک فاصله هستند.
بیضی: مکان هندسی نقاطی که مجموع فواصلشان از دو نقطه ثابت (کانون‌ها) مقداری ثابت است.
کاربردهای مکان هندسی: حل مسائل هندسی، ترسیمات هندسی، و اثبات قضایا.

سوالات پرتکرار در امتحانات:
اثبات مکان هندسی: اثبات اینکه یک مجموعه نقاط، مکان هندسی مورد نظر است.
ترسیم مکان هندسی: ترسیم مکان هندسی با استفاده از ابزارهای هندسی.
حل مسائل هندسی با استفاده از مکان هندسی: حل مسائل مربوط به فاصله، زاویه، و مساحت با استفاده از مفهوم مکان هندسی.
تشخیص نوع مکان هندسی: تشخیص نوع مکان هندسی با توجه به شرایط داده شده.
مسائل مربوط به دایره، خط عمود منصف، نیم‌ساز زاویه، سهمی و بیضی.

نکاتی برای آمادگی در امتحانات:
مطالعه دقیق تعاریف و قضایای مربوط به مکان هندسی.
حل نمونه سوالات امتحانات نهایی سال‌های گذشته.
تمرین ترسیم مکان‌های هندسی با استفاده از ابزارهای هندسی.
درک کاربردهای مکان هندسی در حل مسائل مختلف.
دسترسی به نمونه سوالات امتحانات نهایی سال های گذشته و نمونه سوالات ترم اول در تدریس ریاضی آموزشی مثل قلم چی و همیار آموزش می تواند بسیار مفید باشد.
اگر در هر رشته ای از تحصیل مثل ریاضی دهم هندسه فصل یک ... نیاز به کمک با معلم اینترنتی داشتید, با ما (آموزشگاه ریاضیات و هندسه توربولرن) تماس بگیرید.

سایت تدریس ریاضی: https://tadris-riazi.snails.ir
یوتیوب آموزشگاه ریاضیات توربولرن: https://youtu.be/q02DMN57TF4