تدریس ریاضی

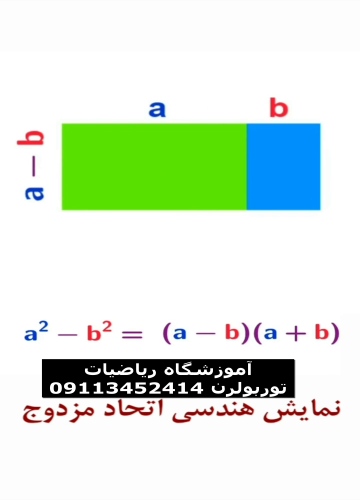
نمایش هندسی اتحاد مزدوج

اتحاد مزدوج می‌گوید: a2−b2=(a+b)(a−b)a^2 - b^2 = (a + b)(a - b)a2−b2=(a+b)(a−b)

برای اینکه این اتحاد را به صورت هندسی (با شکل و مساحت) ببینیم، یک مستطیل تصور کنید که طول آن a+ba + ba+b و عرض آن a−ba - ba−b باشد.

مساحت این مستطیل برابر است با: (a+b)(a−b)(a + b)(a - b)(a+b)(a−b)

حالا اگر داخل این مستطیل یک مربع به ضلع bbb در گوشه‌ها بکشیم (یا بهتر بگوییم، دو مربع به ضلع bbb در دو طرف اضافه و کم کنیم)، متوجه می‌شویم که مساحت باقی‌مانده دقیقاً یک مستطیل به طول aaa و عرض aaa است، یعنی یک مربع به ضلع aaa.

به این ترتیب:

• مساحت کل مستطیل بزرگ: (a+b)(a−b)(a + b)(a - b)(a+b)(a−b)
• اگر دو مربع b×bb times bb×b را کم و زیاد کنیم (در واقع جابجا کنیم)، مساحت باقی‌مانده می‌شود a×a=a2a times a = a^2a×a=a2
• بنابراین مساحت کل برابر است با a2a^2a2 منهای مساحت‌های اضافی که جابجا شدند، یعنی a2−b2a^2 - b^2a2−b2

نتیجه: (a+b)(a−b)=a2−b2(a + b)(a - b) = a^2 - b^2(a+b)(a−b)=a2−b2

این نمایش ساده نشان می‌دهد که چرا ضرب دو عدد مجموع و تفاضل، دقیقاً برابر تفاوت مربع‌هاست؛ چون با جابجایی دو مربع کوچک b2b^2b2، مستطیل بزرگ به یک مربع بزرگ a2a^2a2 تبدیل می‌شود و قسمت‌های جابجا شده دقیقاً 2b22b^22b2 را جبران می‌کنند تا تفاوت a2−b2a^2 - b^2a2−b2 باقی بماند.

این تصویر هندسی یکی از زیباترین راه‌ها برای درک بصری این اتحاد جبری است.

برای درک بهتر ما فیلم نمایش هندسی اتحاد مزدوج را گذاشته ایم که شما با کلیک روی همین خط آنرا میبینید.